A closer look at "training" a trillion-parameter model on Frontier
A paper titled "Optimizing Distributed Training on Frontier for Large Language Models" has been making its rounds over the last few weeks with sensational taglines saying the authors trained a trillion-parameter model using only a fraction of the Frontier supercomputer. The superficiality of the discourse around this paper seemed suspicious to me, so in the interests of embracing my new job in AI systems design, I decided to sit down with the manuscript and figure out exactly what the authors did myself.
As a caveat, I am by no means an expert in AI, and I relied on my friend ChatGPT to read the paper with me and answer questions I had along the way. It is from that perspective that I compiled the notes that follow, and I'm sharing them in the event that there are other folks like me who are interested in understanding how large-scale training maps to HPC resources but don't understand all the AI jargon.
Before getting too far into the weeds, let's be clear about what this study did and didn't do. Buried in the introduction is the real abstract:
"So, we performed a feasibility study of running [Megatron-DeepSpeed] on Frontier, ported the framework to Frontier to identify the limiting issues and opportunities, and prepared a training workflow with an optimized AI software stack."
"...our objective was not to train these models to completion for the purpose of achieving the highest possible accuracy. Instead, our approach was centered around understanding and enhancing the performance characteristics of training processes on HPC systems."
- The authors did not train a trillion-parameter model. They ran some data through a trillion-parameter model to measure training throughput, but the model wasn't trained at the end of it.
- It's worth repeating - they did not train a trillion-parameter model! All the articles and headlines that said they did are written by people who either don't understand AI or didn't read the paper!
- The authors did not create a novel trillion-parameter model at all. This paper wasn't about a new model. There is no comparison to GPT, Llama, or any other leading LLM.
- The authors present a nice overview of existing parallelization approaches for training LLMs. For each approach, they also describe what aspect of the HPC system affects scalability.
- The authors ported a very good LLM training framework from NVIDIA to AMD GPUs. This is a strong validation that all the investment in LLM training for NVIDIA also applies to AMD.
- The authors present a good recipe for training LLMs on hundreds or thousands of GPUs. They tested their approach on transformers with up to a trillion parameters to show that their recipe scales.
This isn't a paper about a new trillion-parameter model. Rather, it is an engineering paper describing how the authors took:
- existing parallelization techniques (data, tensor, and pipeline parallelism)
- an existing training framework that implements those techniques (Megatron-DeepSpeed)
- an existing model architecture that can be made arbitrarily large (a generic, GPT-style transformer)
- existing GPU frameworks, libraries, and packages (CUDA, ROCm, PyTorch, APEX, DeepHyper)
and combined them to all work together, then showed that their approach scales up to at least a trillion parameter and at least a few thousand GPUs.
This paper is also a pretty good crash course on how LLM partitioning strategies translate into HPC system requirements. Let's focus on this latter point first.
Data requirements
Training dataset size
What this line doesn't state is that 20x-200x refers to the number of tokens in the overall training data you can train on before the LLM stops improving. Given that a typical token in an English-language body of data is somewhere between 3 bytes and 4 bytes, we can get a ballpark estimate for how much training data you'd need to train a trillion-parameter model:
- On the low end, 1 trillion parameters * 20 tokens of training data per parameter * 3 bytes per token = 60 terabytes of tokenized data
- On the high end, 1 trillion parameters * 200 tokens of training data per parameter * 4 bytes per token = 800 terabytes of tokenized data
Bear in mind that tokenized data are stored as numbers, not text. 60 TB of tokenized data may correspond to petabytes of raw input text.
Computational power required
The introduction also contains this anecdote:
“A rough estimate [11] tells us that training a Trillion parameter model on 1-30 Trillion tokens will require [...] 6 - 180 Million exa-flops (floating point operations).”
The authors rightly point out that this estimate is rough; the actual requirements are a function of exactly how the LLM's layers are composed (that is, how those trillion parameters are distributed throughout the model architecture), the precisions being used to compute, choice of hyperparameters, and other stuff). That said, this establishes a good ballpark for calculating either the number of GPUs or the amount of time you need to train a trillion-parameter model.
The paper implicitly states that each MI250X GPU (or more pedantically, each GCD) delivers 190.5 teraflops. If
- 6 to 180,000,000 exaflops are required to train such a model
- there are 1,000,000 teraflops per exaflop
- a single AMD GPU can deliver 190.5 teraflops or 190.5 × 1012 ops per second
A single AMD GPU would take between
- 6,000,000,000,000 TFlop / (190.5 TFlops per GPU) = about 900 years
- 180,000,000,000,000 TFlop / (190.5 TFlops per GPU) = about 30,000 years
This paper used a maximum of 3,072 GPUs, which would (again, very roughly) bring this time down to between 107 days and 9.8 years to train a trillion-parameter model which is a lot more tractable. If all 75,264 GPUs on Frontier were used instead, these numbers come down to 4.4 days and 146 days to train a trillion-parameter model.
To be clear, this performance model is suuuuuper sus, and I admittedly didn't read the source paper that described where this 6-180 million exaflops equation came from to critique exactly what assumptions it's making. But this gives you an idea of the scale (tens of thousands of GPUs) and time (weeks to months) required to train trillion-parameter models to convergence. And from my limited personal experience, weeks-to-months sounds about right for these high-end LLMs.
GPU memory required
The limiting factor for training LLMs on GPUs these days is almost always HBM capacity; effective training requires that the entire model (all trillion parameters) fit into GPU memory. The relationship between GPU memory and model parameter count used in this paper is stated:
"training a trillion parameter model requires 24 Terabytes of memory."
This implies that you need 24 bytes (192 bits) of memory per parameter. The authors partially break it down these 24 bytes down into:
- a 16-bit (2-byte) weight
- a 32-bit (4-byte) gradient
- a 32-bit (4-byte) copy of the weight
- a 32-bit (4-byte) momentum (the optimizer state)
That's only 14 of the 24 bytes though, and the authors don't explain what the rest is. That said, other papers (like the ZeRO-DP paper) have a similar number (16 bytes per parameter) and spell out the requirements as:
- a 16-bit (2-byte) weight
- a 16-bit (2-byte) gradient
- a 32-bit (4-byte) copy of the weight for the optimizer reduction
- a 32-bit (4-byte) momentum (one part of the optimizer state)
- a 32-bit (4-byte) variance (the other part of the optimizer state)
Of course, this is all subject to change as models begin to adopt 8-bit data types. The story also changes if you use a different optimizer (the above "optimizer state" components are required by the Adam optimizer), and storing models for inferencing can collapse this down much further since most of these per-parameter quantities are used only during training.
Back to a trillion-parameter model, 24 bytes per parameter would require 24 terabytes of GPU memory, and 16 bytes per parameter would require 16 terabytes of GPU memory. On Frontier, each GPU (well, each GCD) has 64 GB of HBM, meaning you'd need to distribute the model's parameters over at least 256 to 384 GPUs to get the required 16 to 24 TB of HBM required to train one copy of a trillion-parameter model. Of course, training requires other stuff be stored in GPU memory as well, so the actual amount of GPU memory and GPUs would be higher.
LLMs and data structures
At its core, this paper describes how you can distribute this 24 TB model over 256 to 384 GPUs in a way that minimizes data transfer during the training process. To understand the different approaches to partitioning a model, we have to first understand the basic parts of an LLM that must be broken up.
Defining features of an LLM
The paper has a good overview of the transformer architecture, but it details aspects of LLMs that aren't relevant to the work done in the paper itself which tripped me up. The authors used a decoder-only, GPT-style model architecture in their trillion-parameter model architecture, so even though transformers can have encoders and decoders as shown in their figures, all discussion of encoders can be ignored.
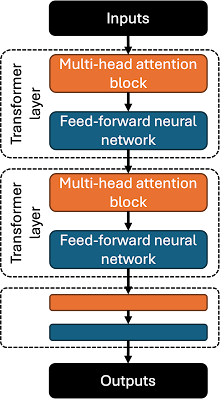
That said, let's talk about the parts of these GPT-style (decoder-only) transformer LLMs. Such transformers are comprised of repeating layers.
Confusingly, a layer of a transformer is not the same thing as a layer in other types of neural networks. Rather, a transformer layer is a repeating block that generally has two sub-components: a multi-head attention block and a feed-forward neural network.
The multi-head attention block is what receives input, and its job is to which parts of that input should get the most focus. It's called "multi-head" because one head establishes focus on one part of the input, and using multiple heads allows multiple areas of focus to be determined in parallel. The output of this attention block encodes information about how different parts of the input are related or depend on each other. Some places refer to a "masked" attention block; this masking is like telling the attention block that it shouldn't try reading an input sentence backwards to derive meaning from it (called "causal self-attention"). Without this masking, inputs are read forward, backward, and in every order in between (establishing "non-causal self-attention").
The feed-forward neural network takes the output of the attention block and runs it through what I think of as a simple multilayer perceptron with a single hidden layer. Note that this feed-forward neural network (FFNN) hidden layer is different than the transformer layer; each transformer layer contains a FFNN, so we have layers within layers here (confusing!). ChatGPT tells me that the FFNN helps establish more complex patterns in the attention block's output.
There's some massaging and math going on between these two components as well, but this outlines the basics of a decoder-only transformer. In practice, you connect a bunch of these transformer layers in series, resulting in a model that, at a very high level, looks like this:
The more transformer layers you use, the more parameters your model will have. It's conceptually very easy to make arbitrarily huge, trillion-parameter models as a result.
Relating parameters to model architecture
The model weights (parameters) of an LLM are contained entirely within the attention block and feed-forward neural network of each layer, and the paper lays them all out.
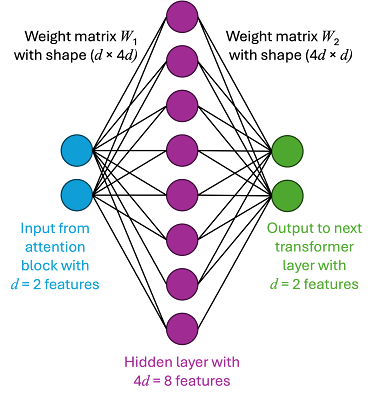
The multi-head attention block has three sets of weight matrices: keys, queries, and values. These matrices have the same x and y dimension (i.e., they're square d × d matrices), and the size of this dimension d (called the hidden dimension) is pretty arbitrary. If you make it bigger, your model gets more parameters. So the number of parameters in each transformer layer's attention block is 3d2.
The feed-forward neural network is a perceptron with a single hidden layer that's typically got 4d features (neurons). Since it takes its input directly from the attention block (which outputs d values) and outputs into the next transformer layer's attention block (which receives d values), the FFNN is comprised of three layers:
The parameters (weights) describe the interactions between the layers, resulting in this FFNN having two matrices containing parameters:
- The weights of the connections between the input layer and the hidden layer are a d × 4d matrix
- The weights of the connections between the hidden layer and the output layer are a 4d × d matrix
So, the number of parameters in each transformer layer's FFNN block is 4d2 + 4d2, or 8d2. This four-to-one ratio of the hidden layer seems arbitrary, but it also seems pretty standard.
The total number of parameters for a single transformer layer is thus 11d2 (3d2 from the attention block and 4d2 + 4d2 from the FFNN). To make a bigger model, either increase the hidden dimension size d or stack more transformer layers (or both!).
The paper points out that "width" and "depth" are the terms used to describe these two dimensions:
"LLMs are transformer models whose shapes are determined linearly by the depth (number of layers) and quadratically by the width (hidden dimension)."
A wider model has a higher d, and a deeper model has more transformer layers. Understanding this is important, because parallelizing the training process happens along these two dimensions of width and depth.
Distributing LLMs across GPUs
The paper goes on to describe three strategies for distributing a model across multiple GPUs:
- Tensor parallelism
- Pipeline parallelism
- Sharded data parallelism
In addition, they also don't ever describe regular (non-sharded) data parallelism even though they use it in the study. Perhaps they viewed it as too obvious to describe, but figuring out a data-parallel approach is an essential aspect to scaling out training of LLMs, so I'll provide my own interpretation of it below.
Following the format of the paper, let's talk about model partitioning from finest-grained to coarsest-grained parallelism.
Tensor parallelism
Tensor parallelism breaks up a model on a per-tensor (per-matrix) basis; in our depth-and-width parlance, tensor parallelism parallelizes along the width of the model.
The paper uses the notation WK, WQ, WV, W1, and W2 to denote the keys, queries, values, and two FFNN parameter matrices; these are what get partitioned and computed upon in parallel. There's a diagram in the paper (Figure 3) which describes the attention half of this process, but it also shows a bunch of stuff that is never described which added to my confusion. To the best of my knowledge, this is what the tensor-parallel computation for an entire attention + FFNN transformer layer looks like:
- The input matrix going into the transformer layer is chopped up and distributed across GPUs.
- Each GPU computes a portion of the attention matrices (WK, WQ, and WV,) in parallel.
- A global reduction is performed to create a single matrix that is output by the attention block. This is an expensive collective.
- The resulting matrix is then chopped up and redistributed across the GPUs.
- Each GPU then uses this chopped-up matrix to compute a portion of the FFNN parameter matrices (W1, and W2)
- Another global reduction is performed to create a single matrix that is squirted out of this layer of the transformer for the next layer to start processing.
I'm leaving out a lot of small transformations that occur between each step, but the high-level point is that tensor parallelism requires a significant number of collectives within each layer to distribute and recombine the parameter matrices.
In addition, the above steps only describe the forward pass through each transformer layer. Once data has finished flowing through all layers in the forward pass, gradients must be calculated, and the backward pass must occur. This means more repartitioning of matrices and global reductions to synchronize gradients for each layer.
The communication demands of tensor parallelism are the reason why NVLink (and Infinity Fabric) exists; the extreme bandwidths (hundreds of gigabytes per second) between GPUs is required to keep the communication overheads of tensor parallelism low enough to prevent the GPUs from stalling out. You effectively cannot implement tensor parallelism outside of a pool of GPUs interconnected with NVLink; conversely, the sum of all the HBM connected to a single NVLink pool limits the size of the LLM with which tensor parallelism can be used. If your model has too many parameters, you can't fit them all in a single NVLink domain with tensor parallelism alone.
The paper shows measurements to back this up; GPU throughput is halved as soon as tensors are split across multiple Infinity Fabric coherence domains on Frontier.
Pipeline parallelism
Pipeline parallelism (or layer parallelism) is a completely different approach. Whereas tensor parallelism partitions the model along the width dimension, pipeline parallelism partitions along the depth dimension. The transformer layers are partitioned and distributed across GPUs, and as data flows through the transformer's layers, it also moves through GPUs. The process goes something like this:
- The entire LLM is chopped up into partitions such that each partition has multiple consecutive transformer layers (entire attention blocks + feed-forward neural networks). These partitions are distributed across GPUs. For example, a twelve-layer LLM distributed over four GPUs would have layers 0-2 on GPU0, 3-5 on GPU1, 6-8 on GPU2, and 9-11 on GPU3.
- A minibatch of training data is chopped up finely into micro-batches.
- Micro-batches are fed into the pipeline of layers for the forward pass.
- Once GPU0 has passed the first micro-batch through layers, GPU1 and its layers begin processing the data.
- At the same time, GPU0 can now begin processing the second micro-batch.
- GPU0 and GPU1 should finish at the same time since they both share equal fractions of the overall transformer. Output from GPU1 moves to GPU2, output from GPU0 moves to GPU1, and a third micro-batch is fed to GPU0.
- When a micro-batch reaches the end of the pipeline and exits the last layer of the transformer LLM, its gradients are calculated, and it begins the backward pass.
- Once the last micro-batch in a minibatch has completed its backward pass, a global reduction performed to synchronize gradients across the entire model. Model weights are then updated using these gradients.
Like with tensor parallelism, the paper shows quantitative results that back up this qualitatively intuitive scaling trend.
If my description of pipeline parallelism and bubbles doesn't make sense without pictures, check out the PipeDream paper which introduced the above process.
Boring old normal data parallelism
Data-parallel training is the easiest way to scale out model training and it is well understood. I strongly recommend reading Simon Boehm's post on the topic to understand its communication requirements and scalability, but in brief,
- Each GPU gets a complete replica of an entire model.
- A batch of training data is chopped it up into minibatches, and each GPU (and each model replica) gets one minibatch.
- Each GPU runs its minibatch through the forward pass of the model. Losses are calculated.
- Each GPU begins the backward pass. After each layer is done calculating its gradients, it kicks off a nonblocking, global synchronization occurs to accumulate all the gradients for that layer.
- After all GPUs have completed their backward passes, those gradients are also all collected and used to update model parameters, then the process repeats.
Sharded-data parallelism
The paper describes sharded-data parallelism only briefly, and it doesn't do any sort of scalability measurements with it as was done for tensor and pipeline parallelism. However, it's a clever way to emulate the process of data parallelism in a way that is very memory-efficient on GPUs, allowing larger models to fit on fewer GPUs. It goes something like this:
- Every layer of the model is chopped up equally and distributed across all GPUs such that every GPU has a piece of every layer. This is similar to tensor parallelism's partitioning strategy.
- The batch of training data is chopped up into minibatches, and each GPU gets a minibatch. This is similar to boring data parallelism.
- To begin the forward pass, all GPUs perform a collective to gather all the pieces of the first layer which were distributed across all GPUs in step #1. This rehydrates a complete replica of only that first layer across all GPUs.
- All GPUs process their minibatch through the first layer, then throw away all of the pieces of that first layer that they don't own.
- All GPUs collectively rehydrate the next layer, process it, and so on. I don't see a reason why all GPUs must synchronously process the same layer, so my guess is that each GPU shares its pieces of each layer asynchronously to whatever layer it is computing.
This process keeps going through all layers for the forward pass, losses are calculated, and then the backward pass is performed in a similar rehydrate-one-layer-at-a-time way. As with boring data parallelism, gradients are accumulated as each layer is processed in the backward pass.
This approach has the same effect as boring data parallelism because it ultimately chops up and trains on minibatches in the same way. However, it uses much less GPU memory since each GPU only has to store a complete replica of one layer instead of all layers. This allows larger models to fit in fewer GPUs in exchange for the increased communication required to rehydrate layers.
On the one hand, this increases the number of collective communications happening, but on the other, it reduces the size of the domain over which these collectives occur. I can see this being useful for designing fabrics that have tapering, since you can fit larger models into smaller high-bandwidth domains.
3D parallelism
The paper makes reference to "3D parallelism" which is really just combining the above partitioning schemes to improve scalability, and in reality, all massive models are trained using a combination of two or more of these approaches. For example,
- You might implement tensor parallelism within a single node so that tensors are distributed over eight GPUs interconnected by NVLink or Infinity Fabric.
- You might implement pipeline parallelism across all nodes connected to the same network switch.
- You might implement data parallelism across nodes sharing the same switches.
So what did they actually do?
The interesting parts of the paper begin in Section IV, where the authors describe using DeepHyper, a tool they developed in 2018, to perform sensitivity analysis on different model partitioning strategies. Their Figure 9 is where much of the money is, and they find that when combining tensor parallelism, pipeline parallelism, and data parallelism:
- Choice of micro-batch size is the most important factor for throughput. Intuitively, this makes sense; getting this wrong will introduces bubbles into the training pipeline where GPUs are idling for a time that's linearly proportional to the micro-batch size.
- Choice of tensor partitioning is second-most important. Again, not surprising since tensor parallelism is very communication-intensive. Interestingly, the authors did not test the sensitivity of this partitioning strategy outside of a single high-bandwidth coherence domain (8 GPUs interconnected with Infinity Fabric) since I presume they knew that would go poorly.
- Choice of layer partitioning is third-most important. This makes sense, as pipeline parallelism isn't as communication-intensive as tensor parallelism.
- Number of nodes follows. They say number of nodes, but my interpretation is that this is really the degree of data parallelism that results from the choice of pipeline and tensor partitioning. Since they used a fixed number of GPUs for this entire parameter sweep, the way they tested didn't really give much room to test the sensitivity to data partitioning as the total degree of parallelism increased. Combined with the fact that data parallelism is the least communication-intensive way to partition training, this low sensitivity isn't surprising.
- Using sharded-data parallelism is least impactful. Although this does introduce additional communication overheads (to reduce the GPU memory required to train), they used the least aggressive form of sharded-data parallelism and only distributed a subset of the matrices (the ones containing optimizer states). My guess is that this only saves a little memory and introduces a little extra communication, so the net effect is that it makes little difference on training throughput.
Based on these findings, they propose a very sensible recipe to use when training massive models: use lots of micro-batches, don't partition tensors across high-bandwidth NVLink/Infinity Fabric domains, and use optimized algorithms wherever possible.
Section V then talks about how they applied this formula to actually run training of a trillion-parameter decoder-only LLM on 3,072 MI250X GPUs (384 nodes) on Frontier. The section is rather short because they didn't run the training for very long. Instead, they just ran long enough to get steady-state measurements of their GPU utilization (how many FLOPS they processed) to show that their approach accomplished the goal of avoiding extensive GPU stalling due to communication.
What didn't they do?
They didn't say anything about storage or data challenges.
Why?
Their brief discussion of roofline analysis says why:
"For these models, our achieved FLOPS were 38.38% and 36.14%, and arithmetic intensities of 180+. The memory bandwidth roof and the peak flops-rate roof meet close to the arithmetic intensity of 1."
Training LLMs is ridiculously FLOPS-intensive; every byte moved is accompanied by over 100x more floating-point operations. This provides a lot of opportunity to asynchronously move data while the GPUs are spinning.
Going back to the start of this post, remember we estimated that a trillion-parameter model might have 80 TB to 800 TB of training data but take months to years to train. The time it takes to move 80 TB of data into hundreds of GPU nodes' local SSDs pales in comparison to the time required to train the model, yet that data transfer time is only incurred once.
But what about re-reading data after each epoch, you ask?
You don't re-read training data from its source at each epoch because that's really slow. You can simply statically partition batches across the SSDs in each node belonging to a model replica and re-read them in random order between epochs, or you can shuffle data between replicas as needed. The time it takes to do these shuffles of relatively small amounts of tokenized training data is not the biggest hurdle when trying to keep GPU utilization high during LLM training.
How valuable is this work?
How novel was the sensitivity analysis? To the AI industry, the answer is "not very." AI practitioners already have an intuitive sense of how the different approaches to parallelization scale since each approach was developed to overcome a previous scalability limitation. Everyone training LLMs in industry is taking this general approach already; they just don't write it down since the industry tends to care more about the outcome of training (a fancy new model) than the mechanical approach taken. That said, I'm sure AI practitioners will find comfort in knowing that the bright minds at Oak Ridge couldn't find a better way to do what was already done, and now this process is documented in a way that can be easily handed off to new hires.
Relatedly, the scientific community will likely benefit from seeing this recipe spelled out, as it's far easier to get access to a large number of GPUs in the open science community than it is in private industry. I could easily see an ambitious graduate student wanting to train a novel LLM at scale, having a healthy allocation on Frontier, and accidentally training in a way that leaves the GPUs idle for 90% of the time.
DeepHyper also sounds like a handy tool for figuring out the exact partitioning of each model layer, across model layers, and across the training dataset during scale-up testing. Regardless of if it's training an AI model or running a massive simulation, the work required to figure out the optimal way to launch the full-scale job is tedious, and the paper shows that DeepHyper helps short-circuit a lot of the trial-and-error that is usually required.
How impactful was the demonstration of training a trillion-parameter LLM on Frontier? I'd say "very."
Sure, running training on a generic, decoder-only, trillion-parameter LLM by itself isn't new or novel; for example, a 30-trillion-parameter model went through a similar process using only 512 Volta GPUs back in 2021. However, to date, these hero demonstrations have exclusively run on NVIDIA GPUs. What this study really shows is that you can train massive LLMs with good efficiency using an entirely NVIDIA-free supercomputer:
- AMD GPUs are on the same footing as NVIDIA GPUs for training.
- Cray Slingshot in a dragonfly is just as capable as NVIDIA InfiniBand in a fat tree.
- NVIDIA's software ecosystem, while far ahead of AMD's in many regards, isn't a moat since the authors could port DeepSpeed to their AMD environment.
- All of the algorithmic research towards scaling out training, while done using NVIDIA technologies, is transferable to other high-throughput computing technology stacks.
What's more, the fact that this paper largely used existing software like Megatron-DeepSpeed instead of creating their own speaks to how straightforward it is to get started on AMD GPUs. No heroic effort in software engineering or algorithmic development seemed to be required, and after reading this paper, I felt like you don't need an army of researchers at a national lab to make productive use of AMD GPUs for training huge LLMs.
With luck, the impact of this paper (and the work that will undoubtedly follow on Frontier) is that there will be credible competition in the AI infrastructure space. Though it might not relieve the supply constraints that make getting NVIDIA GPUs difficult, you might not need to wait in NVIDIA's line if you're primarily interested in LLM training. Frontier represents a credible alternative architecture, based on AMD GPUs and Slingshot, that can get the job done.